The Estimated Posterior Importance Sampling (EPIS) algorithm is described in (Yuan & Druzdzel 2003). This is quite likely the best stochastic sampling algorithm for discrete Bayesian networks available. It produces results that are even more precise than those produced by the AIS-BN algorithm and in case of some networks produces results that are an order of magnitude more precise. The EPIS-BN algorithm uses loopy belief propagation to compute an estimate of the posterior probability over all nodes of the network and then uses importance sampling to refine this estimate. In addition to being more precise, it is also faster than the AIS-BN algorithm, as it avoids the costly learning stage of the latter.
EPIS algorithm can be tuned to improve its accuracy. Its default parameters are listed in the Inference tab of the Network properties dialog. The EPIS algorithm uses Loopy Belief Propagation (LBP), an algorithm proposed originally by Judea Pearl (1988) for polytrees and later applied by others to multiply-connected Bayesian networks. EPIS uses LBP to pre-compute the sampling distribution for its importance sampling phase. Propagation length is the number of LBP iterations in this pre-computation. EPIS uses Epsilon-cutoff heuristic (Cheng & Druzdzel, 2000) to modify the sampling distribution, replacing probabilities smaller than epsilon by epsilon. The table in the Sampling tab allows for specifying different threshold values for nodes with different number of outcomes. For more details on the parameters and how they influence the convergence of the EPI-BN algorithm, please see (Yuan & Druzdzel 2003).
EPIS Sampling algorithm in UAI-2008 inference evaluation
SMILE's implementation of the EPIS Sampling algorithm did well in the UAI-2008 inference evaluation. The following plot show the cumulative error when solving the test instances.
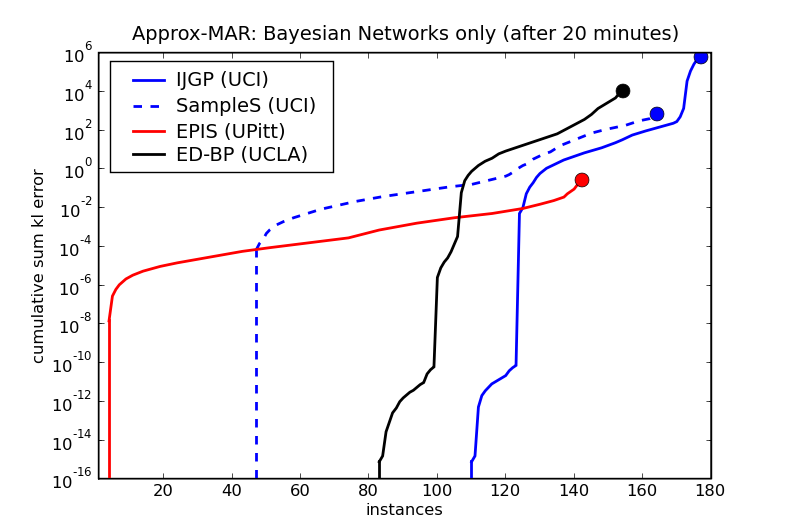
We misunderstood the rules of the competition at the time of submission and did not use exact inference whenever it was possible (for the easiest instances). EPIS Sampling algorithm ran on even the simplest networks and against algorithms that used exact inference on those networks that were computable. Hence, its error on the left-hand side of the graph (the simplest networks) is much larger than that of the other algorithms. Had we used SMILE's clustering algorithm for these simple cases, EPIS's curve (shown in red) would be quite likely close to the x axis. Still, as time progressed and the algorithms faced more difficult cases, EPIS ended up with a lower cumulative error than the other algorithms. Please note that the increase in error between the simplest and more complex instances is not large. See https://www.ics.uci.edu/~dechter/softwares/benchmarks/UAI08/uai08-evaluation-2008-09-15.pdf for the full report.
See also the evaluation results for computing the probability of evidence and marginals in the Probability of evidence and Clustering algorithm sections respectively.