One of the useful possible calculations in a probabilistic model is the (a-priori) probability of evidence. Given a number of observations entered in a network, we ask the question: How likely is this set of observations within this model? To invoke the probability of evidence calculation, choose Probability of Evidence (shortcut CTRL+E) from the Network Menu. or press the Calculate probability of evidence (![]() ) button from the main toolbar.
) button from the main toolbar.
The following dialog displays the results of this calculation:
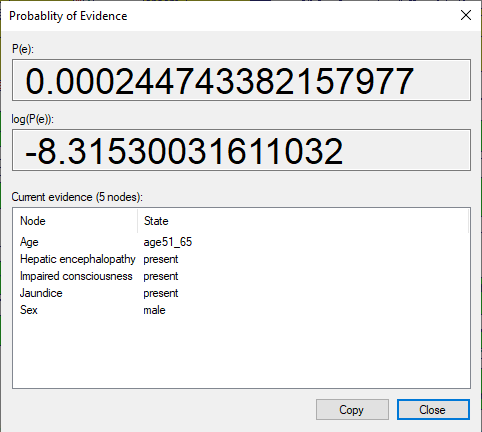
We can see that according to the model at hand, the a-priori probability of observing a male patient between the ages of 51 and 65 with Hepatic encephalopathy, Impaired consciousness and Jaundice is, according to the Hepar II model, roughly 0.000245.
SMILE's probability of evidence algorithm in UAI-2006 and UAI-2008 inference evaluation
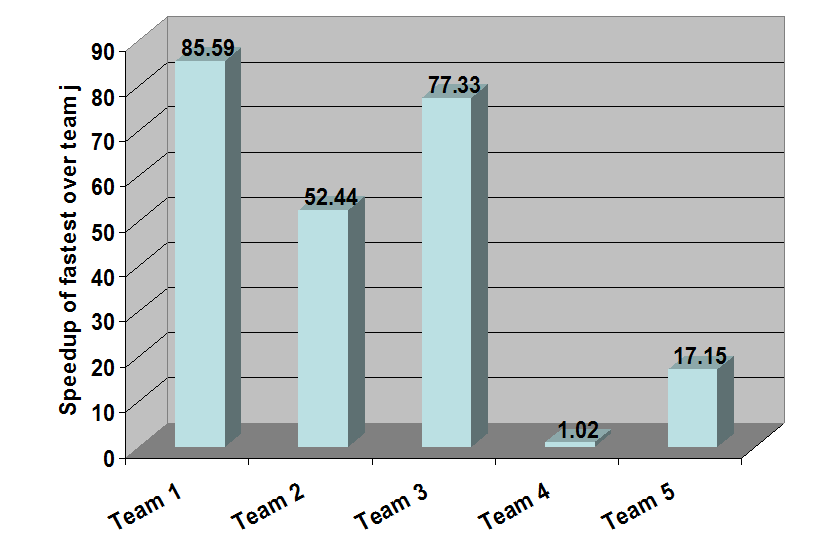
SMILE's probability of evidence algorithm performed very well in the UAI-2006 inference evaluation competition (see https://melodi.ee.washington.edu/~bilmes/uai06InferenceEvaluation/). The following plot shows the average speedup of the fastest team over each of the teams (the lower the bar the better with 1.0 being perfect). SMILE (Team 4) scored 1.02 and was roughly two orders of magnitude faster than other teams. SMILE was slower than the best team's program in less than 2% of the test cases.
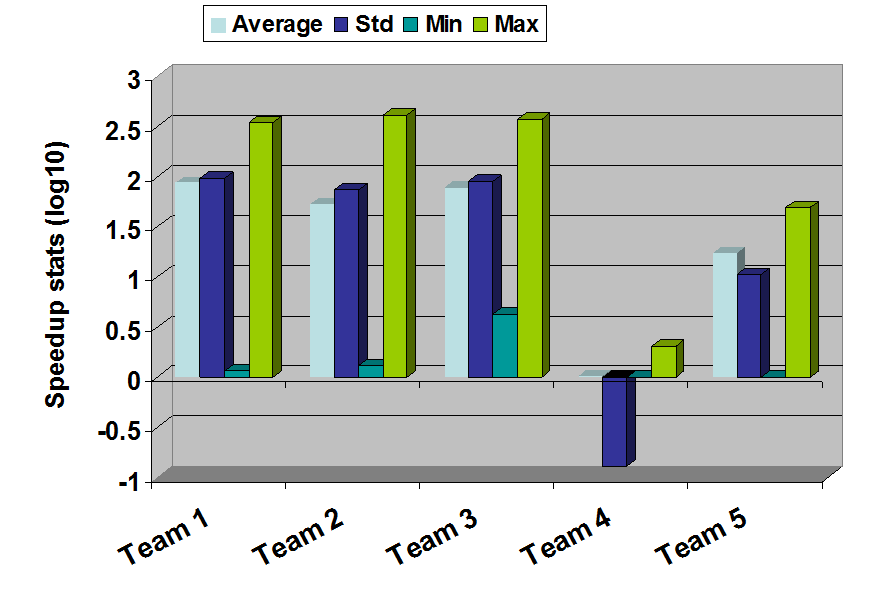
The following plot shows the spread parameters of the speedup (previous plot). SMILE (Team 4) was reliably the fastest with the average standard deviation of 0.01.
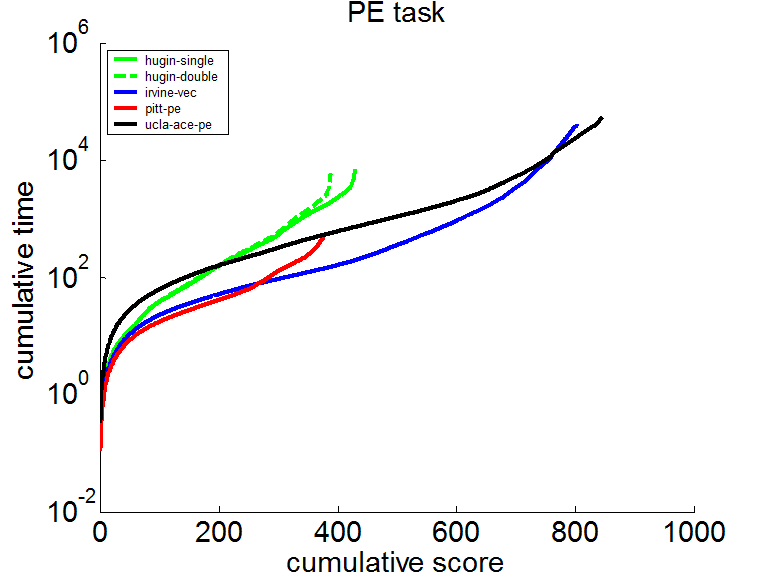
In the UAI-2008 inference evaluation competition (see https://www.ics.uci.edu/~dechter/softwares/benchmarks/UAI08/uai08-evaluation-2008-09-15.pdf for the full report), the algorithm did very well again. SMILE typically computed very fast whatever was computable within a short time. The following plot shows the logarithm of the cumulative time taken over test instances. SMILE was up to roughly half an order of magnitude faster than the other software.
See also the results of computing the exact and approximate marginals in the Clustering Algorithm and EPIS Sampling sections respectively.