The Greedy Thick Thinning (GTT) structure learning algorithm is based on the Bayesian Search approach and has been described in (Cheng et al., 1997). GTT starts with an empty graph and repeatedly adds the arc (without creating a cycle) that maximally increases the marginal likelihood P(D|S) until no arc addition will result in a positive increase (this is the thickening phase). Then, it repeatedly removes arcs until no arc deletion will result in a positive increase in P(D|S) (this is the thinning phase). It is an approximate but a very fast algorithm that yields quite good structures. Here is the Learn New Network dialog for the Greedy Thick Thinning algorithm:
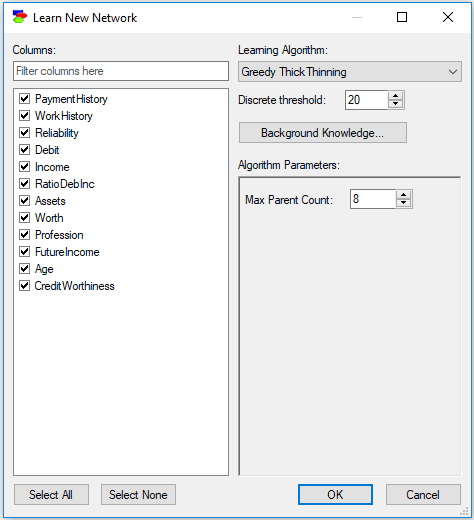
The Greedy Thick Thinning algorithm has only one parameter:
•Max Parent Count (default 8) limits the number of parents that a node can have. Because the size of conditional probability tables of a node grow exponentially in the number of the node's parents, it is a good idea to put a limit on the number of parents so that the construction of the network does not exhaust all available computer memory.
The algorithm produces an acyclic directed graph that gives the maximum score. The score is proportional to the probability of the data given the structure, which, assuming that we assign the same prior probability to any structure, is proportional to the probability of the structure given the data.
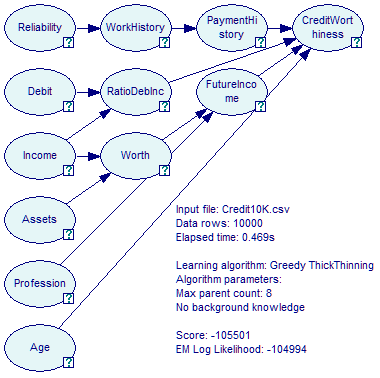
Because the Greedy Thick Thinning algorithm produces an acyclic directed graph, it is a good idea to investigate the theoretical limits to what it can identify based on the data. To this effect, we advise the user to transform the acyclic directed graph of a Bayesian network to the Pattern Editor dialog.