The Noisy-Adder model is described in the doctoral dissertation of Adam Zagorecki (2010) (Section 5.3.1 Non-decomposable Noisy-average). Essentially, it is a non-decomposable model that derives the probability of the effect by taking the average of probabilities of the effect given each of the causes in separation.
To examine the node definition of a Noisy-Adder gate, open the Definition tab among the node's Node Properties.
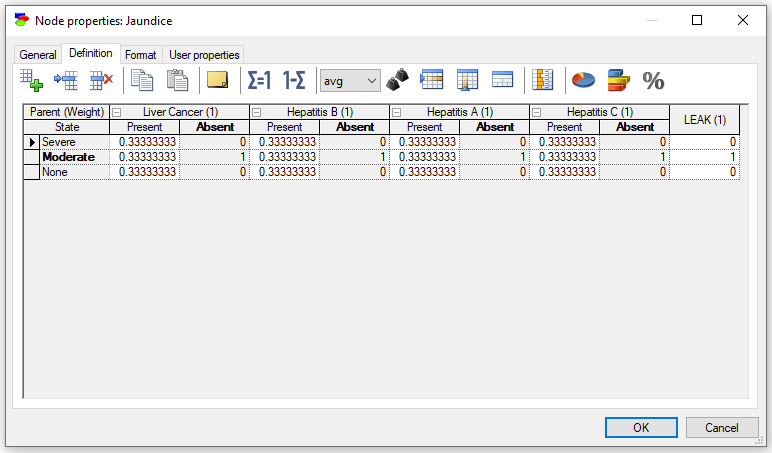
There are two additional buttons on the Definition tab that allow for specifying which of the states of the current node and the parents are the distinguished states.
The Set distinguished state of this node (
) button allows for choosing the distinguished state of the current node. The state with the cursor will become the distinguished state after clicking the button.
The Set distinguished state of parent node (
) button allows for choosing the distinguished state of the selected parent node. The state with the cursor will become the distinguished state after clicking the button.
There are two types of Noisy-Adder nodes: average and single fault, settable through a pop-up menu
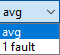
The average-type Noisy-Adder has weights associated with each of the parents. These weights can be edited by invoking the NoisyAdder Weights dialog through the Set weights (
) button.
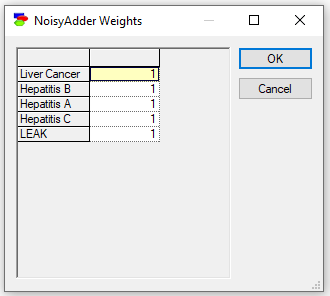
The weight are all equal to one by default and they are displayed in the header of the definition table.
The average-type Noisy-Adder node calculates the CPT from the Noisy-Adder parameters by taking the average of probabilities of the effect given each of the causes in separation. Please note that the leak node (and the leak probability) also take part in this calculation. Each of the nodes is taken with the weight specified in the NoisyAdder Weights dialog. You can examine the CPT that corresponds to the Noisy-Adder definition above by clicking on the Show CPT (
) button. This is the CPT that corresponds to the average type
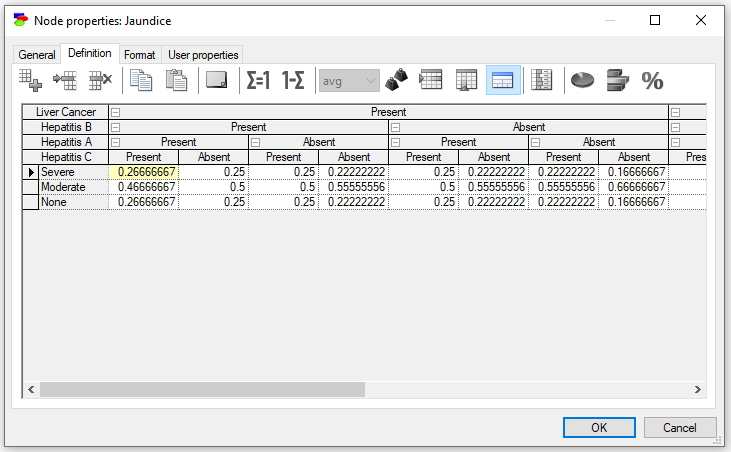
The single fault type Noisy-Adder node assumes that only one of the parent nodes will be in the non-distinguished state. If none of the modeled causes of the effect is active, the Leak node will be active. The CPT corresponding to the definition above looks as follows
Noisy-Adder example
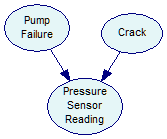
We present here a simple example offered by Adam Zagorecki (2010, pages 106-108) of a diagnostic model of an engine cooling system. Two possible problems, Pump Failure and a Crack in a cooling hose, may impact a Pressure Sensor Reading in the hose, which can be in three states: High, Normal, or Low. The pump can malfunction in two distinct ways: it may work NonStop or simply Fail and not work at all. It may also be fine, which is denoted by its state OK. A Crack in the hose can be Present or Absent. The structure of this problem is as follows:
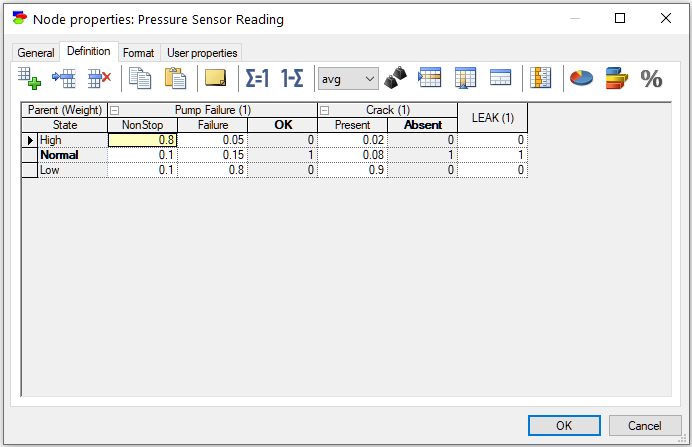
Please note that the Noisy-MAX model is not appropriate here, because the distinguished state of the Pressure Sensor Reading (Normal) does not correspond to the lowest value in the ordering relation. In other words, the neutral value is not one of the extremes, but instead lies in the middle. To apply the Noisy-Adder model, first we need to identify the distinguished states of the three variables, which are naturally OK for Pump Failure, Absent for Crack, and Normal for Pressure Sensor Reading. The next step is deciding whether we should worry about a possible Leak, i.e., influence of unmodeled causes of the Pressure Sensor Reading. When there are no unmodeled causes of Pressure Sensor Reading, we have P(Pressure Sensor Reading=Normal | Pump Failure=OK,Crack=Absent)=1 and the other two states of Pressure Sensor Reading have probability zero. For simplicity, we will assume that there is no Leak. Let the definition of the node Pressure Sensor Reading be the following:
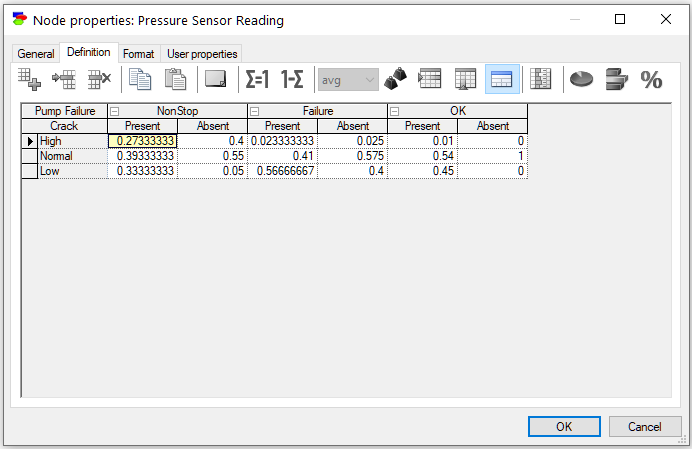
We designate the distinguished states of the parents and the distinguished state of the child node (see Section Chance-NoisyAdder nodes in Node properties). The numbers in the table are self-explanatory and denote the probabilities of the three states of the Pressure Sensor Reading node given various states of each of the parents, assuming that the other parents are in their distinguished states. After all, Noisy-Adder is a canonical model. The CPT expressed by the above definition looks as follows:
Intuitively, the Noisy-Adder node combines the influences of its parents by averaging probabilities. In case where all active influences (i.e., non-distinguished states of the parents) imply high probability of one value, this value will have a high posterior probability and there will be synergy of the causes, similarly to the Noisy-MAX model. If the active parents indicate different states of the effect variable, the combined effect will be an average of the individual influences.