Some outcomes of decision problems involve several, possibly conflicting attributes. For example, outcome of a business decision may optimize productions costs, product quality, company image, and employee satisfaction. While such complex utility structures can be modeled directly by one utility function, it is usually easier for a decision maker to elicit utility functions over each of the attributes in separation and then combine them in a single multi-attribute utility function. MAU functions can be nested hierarchically, so it is possible to have any number of nodes structured hierarchically in such a way that nodes at the next level combine the utilities specified at the previous level.
GeNIe supports two types of multi-attribute utility nodes: (1) general Multi-Attribute Utility (MAU) nodes, which allow any explicitly framed multi-attribute utility function, and (2) a special case of MAU, the Additive Linear Utility (ALU) functions.
To create a MAU node, create a normal Value node first. There are two ways in which such a node can be turned into a MAU node: (1) by right-clicking on the node and choosing Change Type from the menu. Choose MAU or ALU, and (2) when we draw an arc from a Value node to another Value node, GeNIe changes the type of the child node into an ALU node. If MAU is what you want, (1) is the only way you can achieve this transformation.
Consider the following simple model fragment containing four value nodes, three Utility nodes (Income, Growth, and Happiness) and one ALU node (Total Satisfaction), included among the example models as ALU.xdsl.
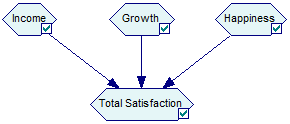
Let us define the coefficient (weights) of the linear multi-attribute additive linear utility function (ALU) in the following way:
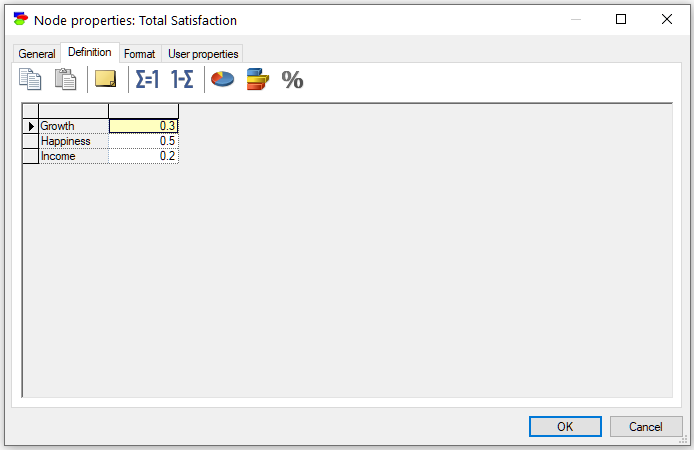
Each of the parent nodes is an ordinary Utility node. The node Total Satisfaction is an ALU node that combines the parent utility nodes using the following linear function:
TotalSatisfaction = 0.5 * Income + 0.1 * Growth + 0.4 * Happiness
Let us change the type of this ALU node into MAU. Here is what the definition looks like now:
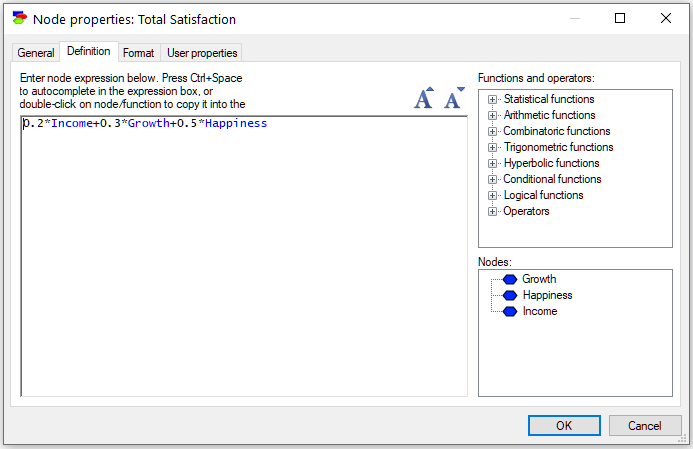
The definition is an equation involving the three parent utility nodes. There are no constraints on this equation, so any functional form can be used here, for example one that expresses the interaction between the three parent utility nodes as multiplicative. MAU nodes are thus as general as they get.
The only parents of ALU and MAU nodes can be utility or other ALU or MAU nodes. There is one exception that is allowed by GeNIe - decision nodes can also be parents of ALU and MAU nodes. Consider the following network fragment
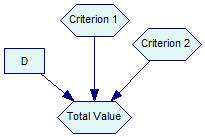
The semantics of such a construct is that the decision node (D) changes the way that utility nodes (Criterion 1 and Criterion 2) interact to produce Total Value. When Total Value is an ALU node, its definition looks as follows
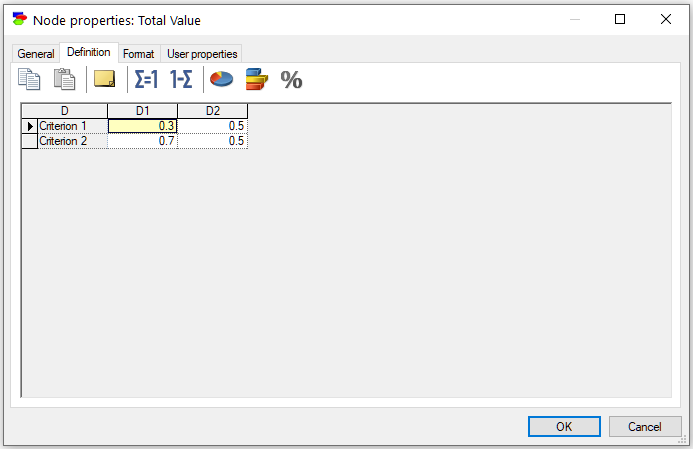
We can see that the weights of the utility nodes (Criterion 1 and Criterion 2) are different for the two decision options D1 and D2. When Total Value is an MAU node, its definition looks as follows
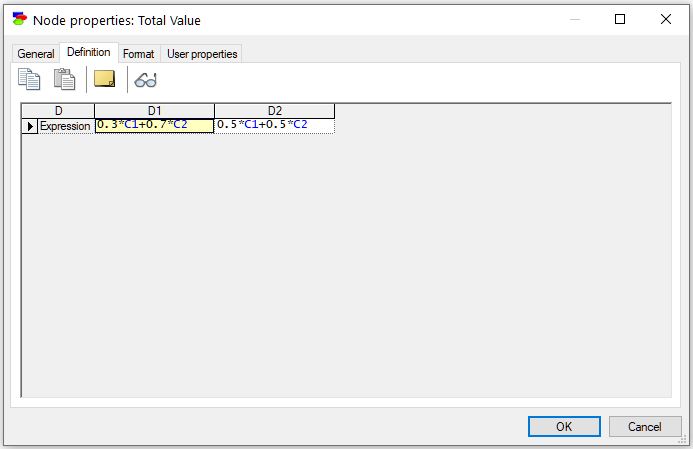
While the two equations in the above model have the same form, just different coefficients, they can be completely different.
There is one more functionality added to GeNIe for user's convenience. GeNIe allows several childless value nodes, which is not really a proper model in decision analysis. This allows for separate optimization over several attributes. In case of such several childless nodes, GeNIe computes the expected utility for each of them, indexed by the states of all decision nodes (i.e., the decision alternatives) and the predecessors of the decision nodes (i.e., nodes that will be observed before the decision is made). The expected utilities can be examined in separation in each of these childless nodes. Expected utility displayed in the decision nodes, however, is a simple linearly-additive combination of the utilities of the childless nodes with the assumption that the weights are all equal to 1.0.