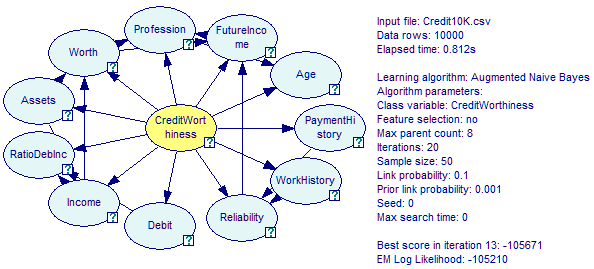
The Augmented Naive Bayes (ANB) structure learning algorithm is a semi-naive structure learning method based on the Bayesian Search approach, described and thoroughly evaluated in (Friedman et al., 1997). The ABN algorithm starts with a Naive Bayes structure (i.e., one in which the class variable is the only parent of all remaining, feature variables) and adds connections between the feature variables to account for possible dependence between them, conditional on the class variable. There is no limit on the number of additional connections entering each of the feature variable, unless it is imposed by one of the algorithm's parameters (Max Parent Count). Please note that this is the main difference between the ABN and the TAN algorithm, which sets the limit on the number of parents to two. The Naive Bayes structure assumes that the features are independent conditional on the class variable, which may lead to inaccuracies when this assumption is violated. The ANB algorithm is simple and has been found to perform reliably better than Naive Bayes. Here is the Learn New Network dialog for the ANB algorithm:
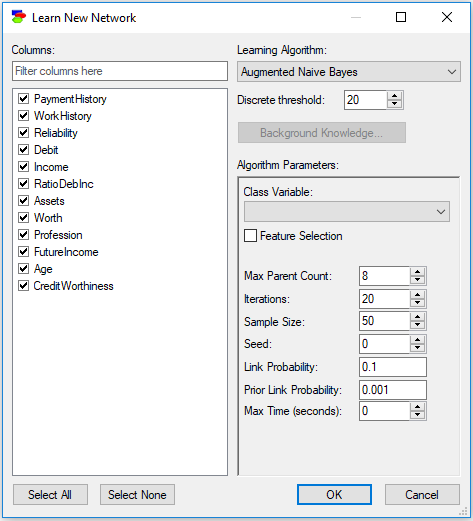
The ANB algorithm has a number of parameters, most of which mimic the parameters of the Bayesian Search algorithm that the ANB algorithm is based on:
•Class Variable, which is a pop-up menu forcing the user to select one of the variables as the class variable. This is a crucial choice, as it determines the structure of the graph. Only those variables that are selected in the Columns list appear on the Class Variable pop-up menu.
•Feature Selection, when checked, invokes an additional function that removes from the feature set those features that do not contribute enough to the classification.
•Max Parent Count (default 8) limits the number of parents that a node can have. Because the size of conditional probability tables of a node grow exponentially in the number of the node's parents, it is a good idea to put a limit on the number of parents so that the construction of the network does not exhaust all available computer memory. When Max Parent Count is equal to 2, the Augmented Naive Bayes algorithm deteriorates in principle to the Tree Augmented Naive Bayes algorithm, which imposes the maximum number of parents of the feature nodes equal to 2.
•Iterations (default 20) sets the number of restarts of the algorithm. Generally, the algorithm is searching through a hyper-exponential search space and its goal can be compared to searching for a needle in a haystack. Restarts allow for probing more areas of the search space and increase the chance of finding a structure that will fit the data better. We advise to make this number as large as we can afford it in terms of running time. The default number of iterations should give you an idea of how long the algorithm will take when the number of iteration is larger. The computing time is roughly linear in the number of iterations.
•Sample size (default 50) takes part in the score (BDeu) calculation, representing the inertia of the current parameters when introducing new data.
•Seed (default 0), which is the initial random number seed used in the random number generator. If you want the learning to be reproducible (i.e., you want to obtain the same result every time you run the algorithm), use the same Seed. Seed equal to zero (the default) makes the random number generator really random by starting it with the current value of the processor clock.
•Link Probability (default 0.1)
•Prior Link Probability (default 0.001)
•Max Time (seconds) (default 0, which means no time limit) sets a limit on the run time of the search phase of the algorithm. It is a good idea to set a limit for any sizable data set so as to have the algorithm terminates within a reasonable amount of time, although it has to be said that the ANB algorithm is quite simple and it is rather unheard of that it does not terminate within a reasonable amount of time.
The algorithm produces an acyclic directed graph with the class variable being the parent of all the other (feature) variables and additional connections between the feature variables. The structure learned is one with the maximum score, similarly to other algorithms based on Bayesian Search. The score is proportional to the probability of the data given the structure, which, assuming that we assign the same prior probability to any structure, is proportional to the probability of the structure given the data.