The continuous Bayesian network used in this tutorial focuses on a fragment of a forced air heating and cooling system. In order to improve the system's efficiency, return air is mixed with the air that is drawn from outside. Temperature of the outside air depends on the weather and is specified by means of a Normal distribution. Return air temperature is constant and depends on the thermostat setting. Damper control signal determines the composition of the mixture.
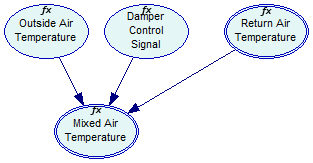
Temperature of the mixture is calculated according to the following equation: tma=toa*u_d+(tra-tra*u_d), where tma is mixed air temperature, toa is outside air temperature, u_d is the damper signal, and tra is return air temperature. Other equation in the model are: tra=24 for return air temperature (which is assumed to be constant), u_d=Bernoulli(0.539)*0.8+0.2 for damper control and toa=Normal(11,15) for outside air temperature. Note the fx symbol above node captions used by GeNIe to indicate that the node is equation-based.
The nodes in this model are created by the helper function CreateEquationNode. It is a modified version of the CreateCptNode used in the previous tutorials. The bold text marks the difference between two functions.
static int CreateEquationNode(
DSL_network &net, const char *id, const char *name,
const char *equation, double loBound, double hiBound,
int xPos, int yPos)
{
int handle = net.AddNode(DSL_EQUATION, id);
DSL_node *node = net.GetNode(handle);
node->SetName(name);
auto eq = node->Def<DSL_equation>();
eq->SetEquation(equation);
eq->SetBounds(loBound, hiBound);
DSL_rectangle &position = node->Info().Screen().position;
position.center_X = xPos;
position.center_Y = yPos;
position.width = 85;
position.height = 55;
return handle;
}
Instead of discrete outcomes, we specify the node's equation and bounds (domain of the node values). The equation is passed as string, which is parsed and validated. For simplicity, we do not check for the status code returned from DSL_equation::SetEquation. In production code, especially if the equation is specified by the user input, you should definitely add a check for DSL_OKAY status. Note that unlike earlier node definition methods, DSL_equation::SetEquation is defined in a class derived from DSL_nodeDef. To call this method, we need to cast the node definition pointer to the DSL_equation type. The easiest way is to use the templated version of the DSL_node::Def method, where the template argument specifies the definition type.
Another helper function, SetUniformIntervals, is used to define the node's discretization intervals. The intervals are used by the inference algorithm when the evidence is set for Mixed Air Temperature node (which has parents). Uniform intervals are chosen for simplicity here; in general case the choice of interval edges should be done based on the actual expected distribution of the node value (for example, in case of the Normal distribution, we might create narrow discretization intervals close to the mean.)
Note that while the model has three arcs, there are no calls to DSL_network::AddArc in this tutorial. The arcs are created implicitly by DSL_equation::SetEquation method (called by CreateEquationNode function).
The network is complete now and we can proceed with inference. The program makes three inference calls, one without evidence and two with continuous evidence specified by calling DSL_nodeVal::SetEvidence(double). Setting the Outside Air Temperature to 28.5 degrees (toa is the name of int variable holding the handle of the Outside Air Temperature node):
net.GetNode(toa)->Val()->SetEvidence(28.5);
This overload of the SetEvidence method is easy to confuse with the one used in previous tutorials, that accepts an integer as a parameter. If the temperature to set had no fractional part, we would need to ensure the literal is of type double by appending ".0":
net.GetNode(tma)->Val()->SetEvidence(21.0);
The program uses UpdateAndShowStats helper function for inference. The helper calls DSL_network::UpdateBeliefs and iterates over the nodes in the network, calling another helper, ShowStats, for each node. ShowStats first checks if the node has evidence set. If it does, the evidence value is printed, and the function returns:
if (eqVal->IsEvidence())
{
double v;
eqVal->GetEvidence(v);
printf("%s has evidence set (%g)\n", nodeId, v);
return;
}
If the node has no evidence, we need to check whether its value comes from the sampling or discretized inference. If sampling was used, the std::vector returned from DSL_valEqEvaluation::GetDiscBeliefs is empty:
const std::vector<double> &discBeliefs = eqVal->GetDiscBeliefs();
if (discBeliefs.empty())
{
double mean, stddev, vmin, vmax;
eqVal->GetStats(mean, stddev, vmin, vmax);
printf("%s: mean=%g stddev=%g min=%g max=%g\n",
nodeId, mean, stddev, vmin, vmax);
}
In such case, the output for the node contains simple statistics from sampling retrieved by DSL_valEqEvaluation::GetStats. To avoid excessive output, we omit the actual sample values, which could be retrieved by DSL_valEqEvaluation::GetSample[s].
If the network had evidence set for the Mixed Air Temperature node (which has parents), the inference algorithm would fall back to discretization, and the discretized belief vector would be non-empty. The else part of the if statement looks as follows:
auto eqDef = node->Def<DSL_equation>();
const DSL_equation::IntervalVector &iv = eqDef->GetDiscIntervals();
printf("%s is discretized.\n", nodeId);
double loBound, hiBound;
eqDef->GetBounds(loBound, hiBound);
double lo = loBound;
for (int i = 0; i < discBeliefs.GetSize(); i++)
{
double hi = iv[i].second;
printf("\tP(%s in %g..%g)=%g\n", nodeId, lo, hi, discBeliefs[i]);
lo = hi;
}
Note how we need to read the discretization intervals specified in the equation node definition to display the complete information about the discretized beliefs (probability comes from node value and discretization interval edges from node definition).
All tutorials redirect SMILE's diagnostic stream to the console, and during the execution of this tutorial the following message will appear on the console when UpdateAndShowStats is called after setting Mixed Air Temperature to 21 degrees:
-19: Equation node u_d was discretized.
-4: Discretization problem in node toa: Underflow samples: 807, min=-39.8255 loBound=-10
Overflow samples: 275, max=72.2534 hiBound=40 Total valid samples: 8918 of 10000
-4: Discretization problem in node tma: Underflow samples: 15145, min=-9.65187 loBound=10
Overflow samples: 8203, max=39.9188 hiBound=30 Total valid samples: 76652 of 100000
The first line with status code -19 (DSL_WRONG_NUM_STATES) is a warning about missing discretization intervals for the Damper Control Signal node. In such case, SMILE uses two intervals dividing the node's domain into two equal halves. Two intervals are adequate in this case, as the equation for this node uses Bernoulli distribution. Status code -4 (DSL_INVALID_VALUE) is a warning that some of the discretization samples fall outside of the node's domain (defined by the lower and the upper bounds set earlier by DSL_equation::SetBounds). Detailed information about underflow and overflow can help during the model building and verification. However, with all unbounded probability distributions and domain bounds determined by physical properties of the modeled system, some of the generated samples will inevitably fall out of bounds.
At the end of the tutorial, the model is saved to disk. Tutorial 8 will expand it into a hybrid network by adding CPT nodes.