Qualitative models in SMILE consist of the DeMorgan nodes. These nodes have DSL_DEMORGAN type and their definition is implemented by DSL_demorgan class. These nodes have always two states (True and False) and can only be linked with other nodes of DSL_DEMORGAN type. While the underlying methodology (and, therefore, DSL_demorgan API) is quantitative and grounded in probability theory, the models can be created interactively in QGeNIe (a simplified version of GeNIe designed to work exclusively with qualitative models) by means of qualitative sliders, colors, and gradients rather than numbers. The color gradients are calculated in QGeNIe based on user preferences, but are based on the numerical output from SMILE, which for DeMorgan nodes are stored in the DSL_beliefVector node value classes (just like DSL_CPT or DSL_NOISY_MAX nodes).
QGeNIe's file format extension is .qdsl. The .qdsl files are supported by DSL_network::ReadFile and WriteFile. Note that DSL_network::WriteFile does not check for the node types in the network and your code should explicitly pass the file name with the .qdsl extension when the network to be saved is qualitative.
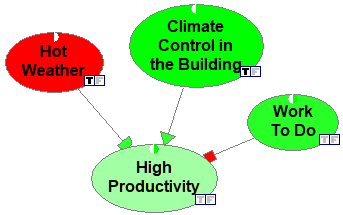
Here is a simple qualitative model displayed in QGeNIe colored with the default green/red palette. The different types of arc heads indicate connection types, described later in this section. T and F icons are used to indicate the node evidence.
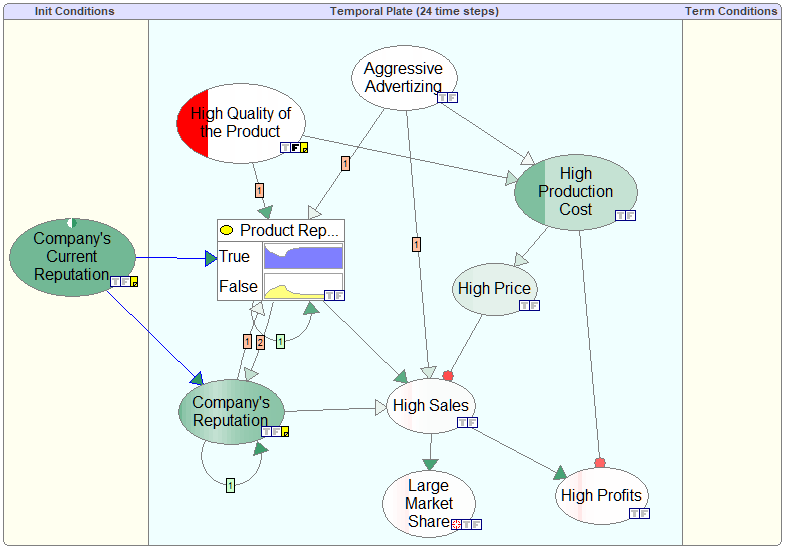
Qualitative models can also be dynamic. The horizontal shading on the plate nodes represents their probabilities changing over time.
Those readers who were exposed to some logic in high school or college know that any logical function can be expressed in one of the Augustus De Morgan's canonical forms, an alternative (OR) of conjunctions (AND) or a conjunction of alternatives. It is also a fact stemming from so called De Morgan laws that the OR function and a negation can express the AND function. A combination of OR functions and negations can express any logical function. QGeNIe's DeMorgan gate offers essentially an intuitive way of expressing any logical function and, in particular, a combination of ORs, ANDs, and negation.
The DeMorgan gate allows for modeling four basic types of influences that one variable (parent in the directed graph) can have on another (a child in the directed graph): (1) a positive influence (a Cause) and (2) a negative influence (a Barrier), both combining with other causes using a noisy OR interaction, (3) a required condition (a Requirement) and (4) a condition that prevents the effect from happening (an Inhibitor), both combining with other causes through an AND interaction.
We will now explain the meaning of the four types of causal influences and how they form any logical function when combined.
•Cause: A cause is a parent that has a positive influence on the child. Please note that this influence does not need to be perfect. For example, smoking is generally believed to be a causal factor in lung cancer. Yet, incidence of lung cancer among smokers, while much larger than incidence of lung cancer among non-smokers, is still within a few percent. Hence, the conditional probability of lung cancer given that a person is a smoker is still fairly low. The cause increases the probability of the effect but does not need to be perfect in its ability to cause it.
•Barrier: A barrier is a parent that decreases the probability of a child. For example, regular exercise decreases the probability of heart disease. While it is a well established factor with a negative influence on heart disease, it is unable by itself to prevent heart disease. One way of looking at a barrier is that it is dual to a cause: Absence of the barrier event is a causal factor for the child. One might go around the very existence of barriers by using negated versions of the variables that represent them. In the example above, one might define a variable Lack of regular exercise, which would behave as a cause of the variable Heart disease. This, however, might become cumbersome if Regular exercise participated in other interactions in a model. It might happen that it is a parent of both Heart disease and Good physical shape. Because Regular exercise decreases the probability of one and increases the probability of the other, Barrier, which is a negated Cause, is a useful modeling construct.
•Requirement: A requirement is a parent that is required for the child to be present. There are perfect requirements, such as being a biological female is a requirement for being pregnant but there are also requirements that are in practice not completely necessary. For example, a sexual intercourse is generally believed to be a requirement for pregnancy, but it is not a strict requirement, as pregnancy may be also caused by artificial insemination.
•Inhibitor: An inhibitor is a parent that prevents the child from happening. For example, rain may inhibit wild land fire. Like in the other types of interactions, the parent may be imperfect in inhibiting the occurrence of the child. Fire may start even if there is rain. Similarly to the relationship between causes and barriers, inhibitors are dual to requirements: Absence of an inhibitor event is a requirement for the child. One might go around the very existence of inhibitors by using negated versions of the variables that represent them. In the example above, one might define a variable No rain, which would behave as a requirement for the variable Wild land fire. This, however, might become cumbersome if Rain participated in other interactions in a model. It might happen that it is a parent of both Wild land fire and Good crop. Because Rain is an inhibitor for the former and a requirement for the latter, Inhibitor, which is a negated Requirement, is a useful modeling construct.
The four types of causes interact with their effect through the following logical formula:
e = (c1 ∨ c2 ∨ …∨ ¬b1 ∨ ¬b2 ∨ …) ∧ r1 ∧ r2 ∧ … ∧ ¬i1 ∧ ¬i2 ∧ … ,
where cis are Causes, bis are Barriers, ris are Requirements and iis are Inhibitors.
For the DeMorgan node API details, see the DSL_demorgan reference. QGeNIe manual is available at BayesFusion's documentation website https://support.bayesfusion.com/docs and contains a detailed description of qualitative models, including references to research papers.